There are few problems in math as stubborn as the Riemann hypothesis. First proposed in 1859, there have been dozens of attempts at solving it, by some of the sharpest mathematical minds around – but all have come up short.
Results on the hypothesis, therefore, when they do come, tend to be a bit… sideways. Mathematicians don’t tackle the problem head-on – they wouldn’t even know where to start, in fact, even today – so instead, they answer other, smaller, related questions. Answer enough of these, they hope, and perhaps it will one day add up to a proof of Riemann’s original statement.
But unfortunately, even these baby steps are rare. So when a pair of mathematicians posted a new paper in May that claimed to have improved a result on the hypothesis that has held firm for more than eight decades, it’s no surprise it caused some real excitement in the mathematical community.
So… what’s the big deal?
What is the Riemann hypothesis?
There are two ways to answer the question “what is the Riemann hypothesis?”, and which one you get will kind of depend on why you’re asking.
The more direct, but frankly less helpful, answer is this: the Riemann hypothesis is a conjecture from number theory which states that the nontrivial Riemann zeta function zeros all lie on the “critical line” σ = 1/2.
Now, clearly there’s some terminology to crack open there, the most important of which is that “Riemann zeta function”. Defined over the complex numbers – that is, numbers that have both a real and an imaginary part – the Riemann zeta function is basically an infinite sum of fractions taken to a complex power. And yes, it’s about as esoteric to work out as you’re imagining.
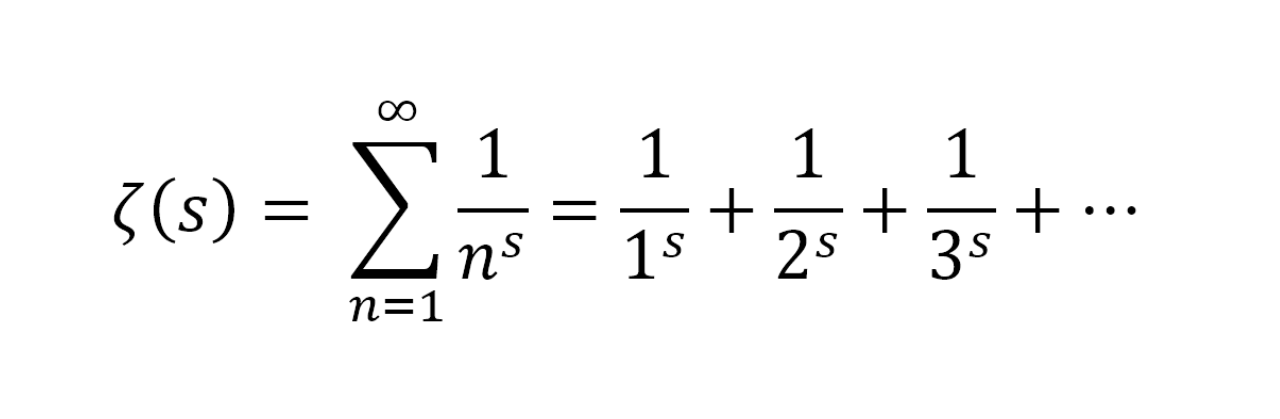
The Riemann zeta function expressed as a series.
Image Credit: IFLScience
Regardless, it can be evaluated, and we do actually know the first, oh, ten trillion or so solutions. Here’s the thing, though: almost all of them are totally useless and uninteresting to us, because the next most important bit of the hypothesis is where it says “nontrivial zeroes”.
See, it turns out there’s a whole bunch of inputs for which this big sum evaluates to zero – that is, ζ(s) = 0. Some of those aren’t that interesting – specifically, whenever s is a negative even real number, like -2, -4, -6, and so on – and we call those “trivial”. We don’t care about those. But the others? Well, that’s where things get interesting.
As far as anyone can tell, every one of these “nontrivial” zeroes has one thing in common: its real part is equal to 1/2. And really, that’s all the Riemann hypothesis says: it’s the statement, as yet unproven, that this is always true – that every nontrivial zero of the zeta function lies somewhere on the “critical line” of s = 1/2 + iy.
Now, at this point in the discussion, you’re probably asking a pretty important question, which is: why the heck should anybody care about this? And that’s fair – so far, it looks like a very niche and extremely abstract problem. But the exciting thing about the Riemann hypothesis isn’t actually what it says – it’s what it means.
“The Riemann Hypothesis seeks to understand the most fundamental objects in mathematics – prime numbers,” wrote University of Oxford mathematician Marcus du Sautoy in his 2003 book The Music of the Primes.
“Prime numbers are the very atoms of arithmetic […] those indivisible numbers that cannot be written as two smaller numbers multiplied together,” he explained. “For mathematicians they instill a sense of wonder.”
We know: at first glance, all those complex values and infinite sums don’t appear to have too much to do with prime numbers. So, what’s the connection? Well, it all comes down to the question of where primes turn up on the number line – or, more accurately, how frequently they turn up along the number line.
See, prime numbers may be the building blocks of math, but they’re pretty finicky things too. Unlike, say, even numbers, or square numbers, or, heck, even supernatural numbers, there’s simply no way to predict where or when they turn up – “things just seem to get worse the higher you count,” wrote du Sautoy; “in fact, [the] procession of primes resembles a random succession of numbers much more than it does a nice orderly pattern.”
But this impenetrable nature just prompted mathematicians to come at the problem from a different direction. Maybe we can’t say much about exactly where the primes turn up, but we can say something about how many of them occur below some arbitrary number N: it’s roughly N/log(N).
But exactly how “rough” is “roughly”? Well, that’s the question that the Riemann hypothesis would answer. Prove that every nontrivial zero has a real part of 1/2, and you’ve found the best possible bound for the error margin of that estimate. And that, as we’ll see later, is something very exciting indeed.
What is the breakthrough?
Ever since Bernhard Riemann first proposed his eponymous hypothesis, mathematicians have been scrambling to prove it one way or the other – but despite quite a few highly-publicized claims over the years, nobody has succeeded.
What we have been able to do, though, is squish the problem. Riemann himself was able to show that the real parts of the nontrivial zeroes were all between 0 and 1, and he also knew that they held a mirror symmetry around the 1/2 line – two pieces of information that transform the scale of the problem from “the entire real number line” to “the bit of the real number line between 1/2 and 3/4.”
Then, in 1940, the British mathematician Albert Ingham chipped away a little further at the problem, proving an upper limit on the number of zeroes that could exist with a real part of 3/4. It seemed like we were, albeit slowly, making some progress on the problem.
And then… we got stuck again. “It was a bit outrageous that this [limit] could not be lowered,” Maksym Radziwill, a math professor at Northwestern University who specializes in number theory, told Science last week. “Basically, nobody was working on this because everybody gave up.”
Everybody, that is, except James Maynard, a professor of Number Theory at the Mathematical Institute at the University of Oxford, and one of the authors of the recent paper. At a meeting of the American Mathematical Society in early 2020, he was struck by an intriguing idea: maybe the problem could be tackled using harmonic analysis, a type of math that studies functions by representing them as frequencies.
It was a serendipitous meeting. Also in attendance was Larry Guth, a professor of mathematics at MIT and an expert in precisely that field. He, too, had a hunch that harmonic analysis might help add a crack to the Riemann problem – but unfortunately, he “didn’t know the analytic number theory at all well,” he told Quanta last month. It was, essentially, a match made in mathematical heaven: Maynard had the theory, and Guth had the toolbox. Could they build a solution to this 175-year-old problem?
Well… no. In the end, it turned out that harmonic analysis wasn’t the silver bullet either had hoped – but so much time spent contemplating the problem from new and unorthodox angles paid off regardless. By translating the problem into yet another mathematical language, the pair managed to reduce it to a question about matrices and eigenvalues – things that “mathematicians love to see,” Guth told Quanta, “because matrices are one of the things that we understand really well.”
The goal now was to find a limit on how big the eigenvalues of certain matrices could get – a process that basically involved trying to simplify and cancel out as much of a very complicated sum as possible. And in this already unconventional approach, the pair made some surprising decisions: “We do something that at first sight looks completely stupid. We just refuse to do the standard simplification,” Maynard explained.
“In chess you call it a gambit,” he told Quanta. “You sacrifice a piece to get a better position on the board.”
And in just a matter of months, the pair had a kind of checkmate: an upper limit on the largest eigenvalue – and at long last, an improvement on the bound that Ingham had found more than 80 years earlier.
“This might actually restart an area that was really neglected for a long time,” Radziwill told Science. “I mean, there could be a Renaissance.”
Why is that important?
Short of winning yourself a million dollars, it’s perhaps hard to imagine what real-world impact solving the Riemann hypothesis might have. But don’t underestimate it: “a proof of the Riemann Hypothesis would mean that mathematicians could use a very fast procedure guaranteed to locate a prime number with, say, a hundred digits or any other number of digits you care to choose,” explained du Sautoy.
And while “finding hundred-digit primes sounds as pointless as counting angels on a pinhead,” he pointed out, it’s actually incredibly important – to more or less every part of our lives today. They’re a crucial ingredient in the field of cryptography, which in turn keeps just about everything online secure – from the moment your browser authenticates itself to the server you’re trying to access (and vice versa), you’re relying on prime numbers to keep your data safe.
“Every business trading on the Internet […] depends on prime numbers with a hundred digits to keep their business transactions secure,” du Sautoy wrote. “Suddenly there is a commercial interest in knowing how a proof of the Riemann Hypothesis might help in understanding how primes are distributed throughout the universe of numbers.”
Of course, we’re getting well ahead of ourselves. It is, to put it mildly, very unlikely that this new breakthrough is going to solve the entire hypothesis – and for mathematicians, that’s not really the point in any case. After all, nobody really thinks the Riemann hypothesis is false – but “a proof gives much more than just a statement being true,” Maynard told Science. “It gives an understanding as to why it’s true, so you have some powerful new technique for understanding prime numbers.”
And so maybe Maynard and Guth’s result isn’t, on the face of it, a huge breakthrough – but, like the hypothesis itself, it’s what it means that’s more important than what it literally says. The strategies they used have the potential to unlock far more than just prime number theory: mathematicians are already pouncing on the techniques to simplify results and problems in fields as diverse as dynamical systems, geometry, and even wave physics.
In short, the result is nothing less than “sensational,” Alex Kontorovich, a math professor at Rutgers University, told Science.
“There are a bunch of new ideas going into this proof that people are going to be mining for years.”
The paper is posted to the pre-print server Arxiv.
Source Link: A Million Dollar Math Puzzle Just Got A Little Bit Closer To A Solution