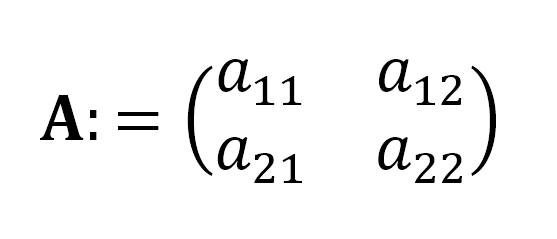For most of us here in the 21st century, our memories of learning the times tables have become something of a running joke. “You won’t have a calculator in your pocket every day as an adult,” we were warned – well, shows what you know, Mrs Hickinbottom; these days, virtually 100 percent of us have not just a calculator in our pocket, but access to the entirety of collected human knowledge so far.
Mathematicians and computer scientists, though, are not most people. Ever since at least the early 19th century, there’s been a new kind of multiplication in town: matrix multiplication – and even today, with all our technological prowess, it’s a real ballache.
But does it have to be? A pair of new results – one from November 2023, and a second which was published in January – hint that the answer is “no” – or at least, “not as much as we previously thought.”
The problems with matrix multiplication
So, first question: what actually is a matrix? Unfortunately, the answer is way less cool than the movie adaptation made it seem.
Put simply, a matrix is just a rectangular array of numbers – or other mathematical objects like symbols or expressions or even other matrices, because sometimes we all feel a bit masochistic – arranged in rows and columns. They have a really wide range of uses in math and science, so being able to manipulate them is… well, pretty important.
A matrix.
Image Credit: IFLScience
Now, multiply two matrices together, and you’ll get another matrix – so long as a few stipulations are satisfied. First of all, you can only multiply two matrices together if the number of columns in the left matrix is the same as the number of rows in the right matrix, like this:
Two matrix multiplication problems.
Image Credit: IFLScience
Getting that right is important because, unlike normal multiplication, the matrix operation is not commutative – that is to say, order matters. Given two matrices A and B, it’s completely possible that you might be able to work out the matrix product AB but not BA; even if both are possible, there’s no particular reason that they would give the same answer.
Two matrix products showing the noncommutativity of matrix multiplication.
Image Credit: IFLScience
So, once we’ve got all these requirements out of the way, how do we actually go about finding the product of two matrices? In mathematical notation, the answer looks like this:
Easy peasy.
Image Credit: IFLScience
Which, we admit, may not actually be too helpful. So let’s look at an example.
First row, first column; first row, second column; second row, first column; second row, second column. It’s much more complicated after 2-by-2 matrices though.
Image Credit: IFLScience
You might be getting the idea by now that matrix multiplication involves a lot more work than regular multiplication – and you’d be completely right. That’s one reason why having a computer program that could do it all for us would be such a boon – except as it turns out, even that is a problem.
The slow march of progress
“Ever since the dawn of the computer age, researchers have been trying to find an optimal way of multiplying matrices, a fundamental operation that is a bottleneck for many important algorithms,” explained Sara Robinson for SIAM News in an article on the problem from 2005.
“Faster matrix multiplication would give more efficient algorithms for many standard linear algebra problems, such as inverting matrices, solving systems of linear equations, and finding determinants,” the article continues. “Even some basic graph algorithms run only as fast as matrix multiplication.”
So the question becomes: just how fast is that? And the answer, sadly, is “not all that fast at all, historically.” Given a couple of matrices with, say 100 rows and columns each, you’ll need to perform 1,000,000 multiplications to find their product – and that number increases cubically, not linearly. In other words: increase those matrices by just a single row and column, and the number of multiplications needed to solve the problem goes up by more than 30,000.
Now, that’s not to say we can’t do it faster – and indeed, quite a lot of research has gone into figuring out ways to do so over the years. Most experts in the field think we’ll eventually top out at quadratic time: that it should be possible to multiply a pair of 100-by-100 matrices using 10,000 steps, but not fewer. But exactly how to achieve that is still a major open problem in computer science.
“The point of this work,” Renfei Zhou, theoretical computer science student at Tsinghua University and co-author on the new papers, told Quanta Magazine earlier this year, “is to see how close to two you can come, and whether it can be achieved in theory.”
We’ve made some headway. Since 1969, when mathematician Volker Strassen made the first inroad into a more efficient algorithm for matrix multiplication, that time exponent has gone from three down to below 2.4 – or to put it another way, requiring fewer than 64,000 calculations to multiply those 100-by-100 matrices together. But it’s been tough going – and since the late eighties, improvements have been “small and […] extremely difficult to obtain,” Nagoya University computer scientist François Le Gall told Quanta.
So, you may be thinking, why should we be excited about some new refinement? After all, from a purely numerical perspective, the gain isn’t even that notable.
And yet, the breakthrough is “conceptually larger than other previous ones,” Le Gall told Quanta. So what makes it so special?
Improving on the best
To understand the hurdle that was cleared between November and January, we ought to take a look at the situation beforehand – and as it turns out, it was a bit of a hodgepodge.
In 1986 and 1987, two major breakthroughs occurred: first, Volker Strassen – yes, him again – came up with what is now known as the laser method for matrix multiplication; then, a year later, computer scientist Shmuel Winograd and cryptographer Don Coppersmith developed an algorithm specifically designed to complement and improve upon Strassen’s work.
The result of combining these two techniques is quite ingenious. Strassen’s original contribution, back in the ‘60s, was to notice that by rewriting matrices A and B in terms of block matrices – that is, considering them to be matrices whose elements are other matrices – their product A∙B = C can be found in fewer than n3 calculations as long as you perform the right calculations.
Figuring out what you need to do, then, is where Coppersmith and Winograd come in. Their algorithm “tells me what to multiply and what to add and what entries go where,” Virginia Vassilevska Williams, a computer scientist at the Massachusetts Institute of Technology and co-author of one of the new papers, told Quanta. “It’s just a recipe to build up C from A and B.”
And this is where the laser method comes into play. While Coppersmith and Winograd’s algorithm is brilliant, it’s not perfect; it generally results in some redundancies, with various terms “overlapping” here and there. The laser is how computer scientists aim to “cut out” these duplicates: it “typically works very well,” Le Gall said, “and generally finds a good way to kill a subset of blocks to remove the overlap.”
But like an early-2000s beautician faced with a pair of natural eyebrows, sometimes you can laser away too much. “Being able to keep more blocks without overlap thus leads to […] a faster matrix multiplication algorithm,” Le Gall told Quanta – and it’s precisely that realization upon which Duan’s team’s technique hinges.
Rebalancing the scales
By modifying the way the laser method assigns weight to the blocks in a matrix – how important it deems them, and therefore how likely they are to be kept rather than cut out – the team managed to reduce the calculation time for matrix multiplication by the most significant amount in more than a decade.
Now, don’t get too excited – they only brought it down from 2.373 to 2.372. But that isn’t really the point: what’s got computer scientists excited isn’t the result achieved, but how the team did it. After close to forty years of infinitesimally small improvements on the same combination of algorithms, Le Gall told Quanta, “they found that, well, we can do better.”
Just how much better remains to be seen – but if you’re wondering what practical applications you can expect to see these groundbreaking results being applied to, you might find yourself a little disappointed. The laser method itself is already what’s known as a “galactic algorithm” – so named because it’s never used for any problems on Earth – and barring some massive unforeseen change in the status of quantum computing, the same will inevitably be true for the new improved versions.
“We never run the method,” confirmed Zhou. “We analyze it.”
Source Link: Chasing Perfection In A Long-Standing Theoretical Computing Riddle