Modern math problems don’t tend to have the kind of answers that trip off the tongue. Perhaps it’s a brand-new proof that takes a few pages’ worth of words and diagrams to explain properly, or an improvement on a previous result that’s so specific as to be virtually invisible. Maybe it’s entirely dependent on a different result that will likely never get solved, so what’s even the point?
It’s rare that a big ol’ math problem will have an answer like, say, “15”, is what we’re getting at. Unless, that is, it’s the one recently solved by grad student Bernardo Subercaseaux and professor Marijn Heule, both from Carnegie Mellon University’s math department, who have finally come up with the solution to a problem originally posed all the way back in 2002.
So, what was the question? Like many of the most difficult math problems, it doesn’t sound like it should be too difficult: the goal is to fill a grid with numbers in such a way that the distance between any two squares containing the same number is larger than that number.

For example, in the infinite path – a one-dimensional infinite grid – no two adjacent squares may both contain “1”, as the distance between two “1”s must be greater than one. Similarly, the distance between two “2”s must be greater than two, and so on.
Image Courtesy Of Bernardo Subercaseaux
The real question, though, is something a little more specific: it’s to find the smallest number of numbers needed to complete this grid.
There’s a pretty good reason that problem hadn’t been solved yet: “Trying to do this brute force would take until the universe finishes if you did it naïvely,” Wayne Goddard, a Professor in Clemson University’s School of Computing and one of the originators of the problem more than two decades ago, told Quanta Magazine.
“So you need some cool simplifications to bring it down to something that’s even possible,” he said.
So that’s exactly what Subercaseaux and Heule did. Heule had already made his name finding efficient ways to locate solutions for long and complex math problems, and Subercaseaux had been tinkering with the question in his spare time using a Minesweeper-like tool he had asked a friend to build for him. While the sheer physics of the problem were potentially overwhelming, the duo believed that with a little mathematical nous, a solution could be possible.
“We had several promising ideas,” Subercaseaux told Quanta. “So we took the mindset of ‘Let’s try to optimize our approach until we can solve this problem in less than 48 hours of computation on the cluster.’”
One of the first big breakthroughs, strangely, wasn’t even one of their own. The pair quickly found that the solution they were searching for had to be larger than 12 and smaller than or equal to 15 – a result that would have been very significant, had it not been originally discovered some four or five years earlier.
“To my absolute horror […] a bunch of the results I had proved were already known, spread out over [dozens] of papers,” Subercaseaux wrote in a blog post on the result earlier this year.
He was “extremely nervous” about it, Subercaseaux continued. “But Marijn’s reaction was incredible […] He was happy that other people cared about the problem, and he was happy that the original core part of the problem, that of determining the packing-chromatic number of the infinite square grid, was still open. Needless to say, I was very relieved.”
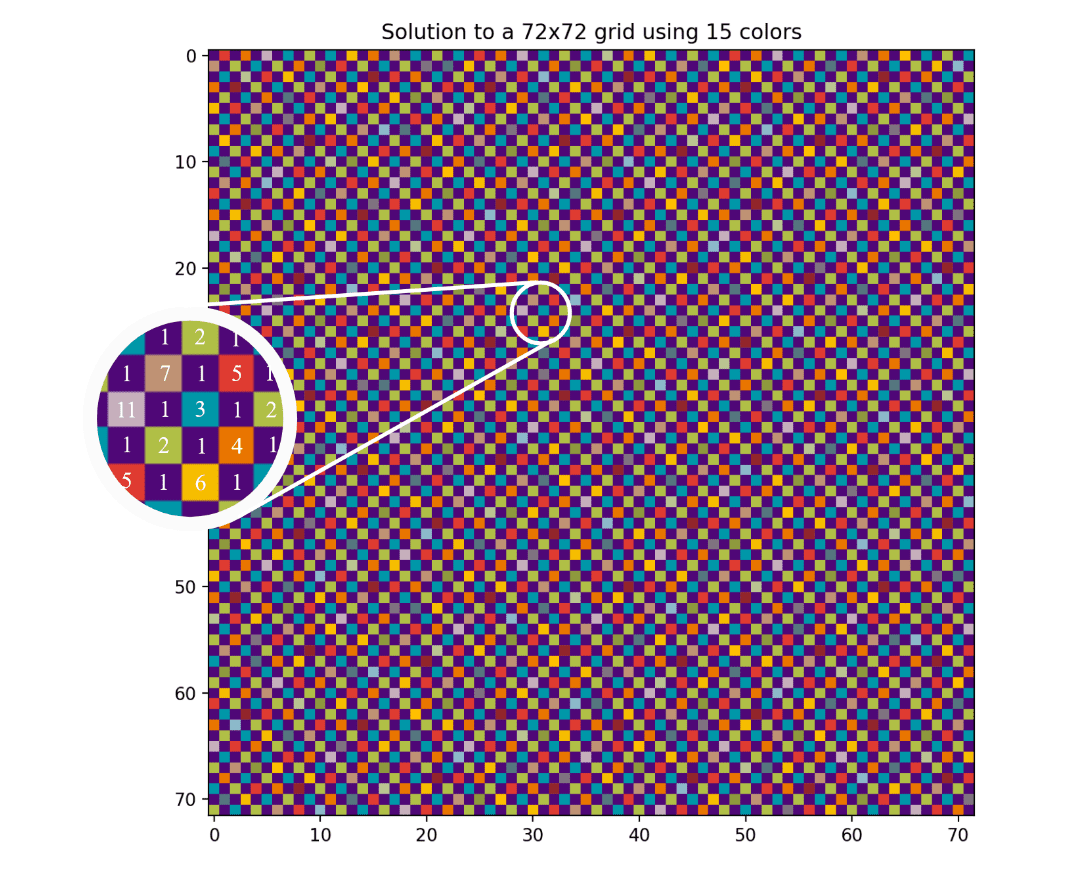
A periodic coloring for a 72-by-72 grid containing 15 colors – thus showing that the answer is at most 15.
Image Corutesy Of Bernardo Subercaseaux
With the range of possible answers reduced from any number to either 13, 14, or 15, the pair set out to reduce the computational time for potential solutions. The first shortcut they found was to exploit symmetry: by treating all symmetric solutions as equivalent, they were able to cut the time spent searching for a solution by a factor of eight.
Adding to that a technique previously developed by Heule called “cube and conquer” allowed the two-man team to rule out 13 as a solution in less than two days’ computation time. The number of possible solutions had been reduced by one-third – if they could just rule out either 14 or 15, the problem would finally have its answer.
To do that, however, the pair would need even stronger optimization techniques. “We pretty much needed to optimize our computation by a factor of roughly 100,” Subercaseaux wrote. “Note that a really nice optimization idea sometimes gives you a factor of 2, so you’d need 7 of those ideas to improve by a factor of 100!”
The key, it turned out, was to consider small regions of the grid rather than individual cells: instead of considering the problem square-by-square, they instead split it into plus-shaped groupings of five squares at once.
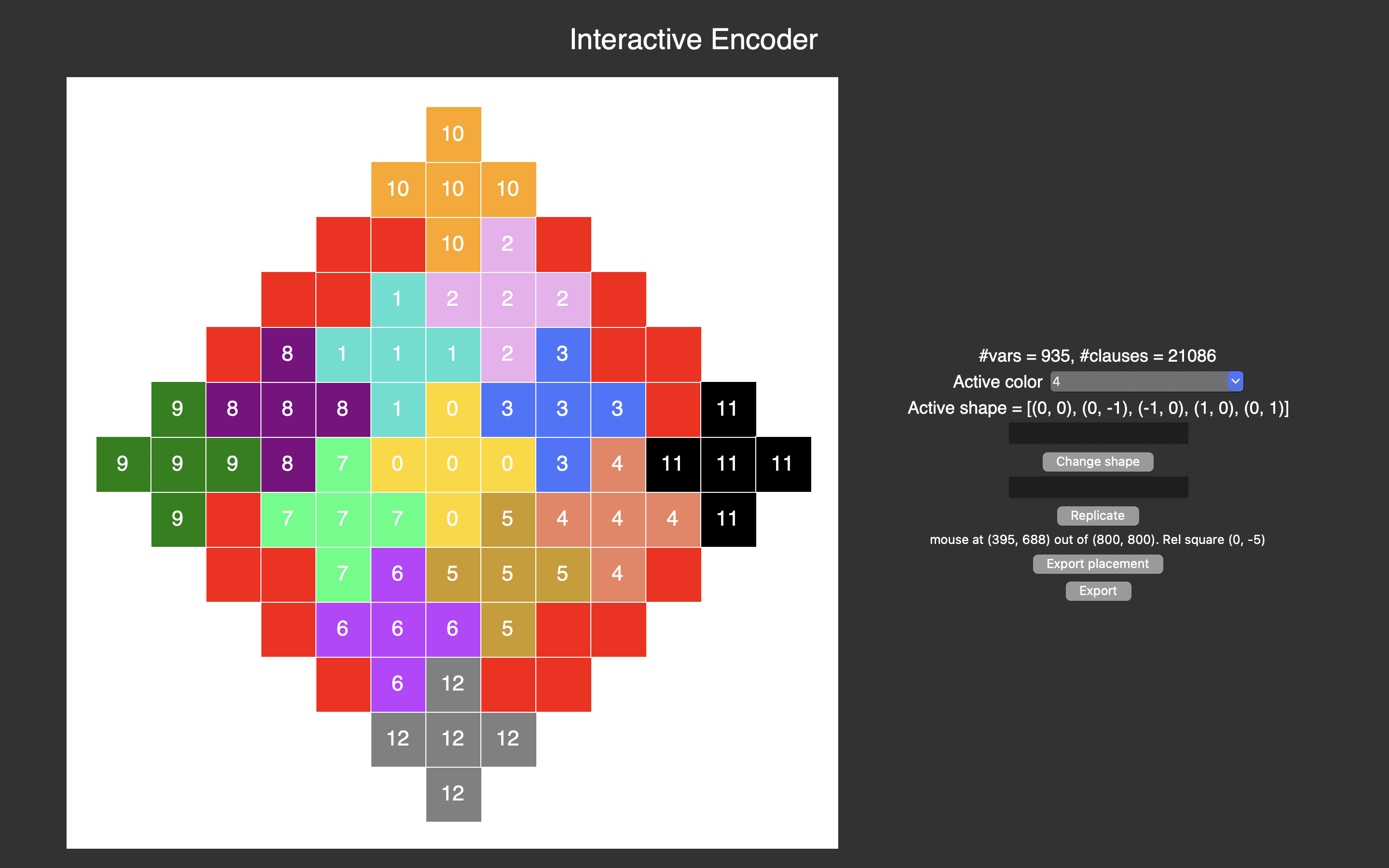
A screenshot of Interactive Encoder, a tool built by Subercaseaux for the project, showing the “plus” method.
Image Courtesy Of Bernardo Subercaseaux
It was a breakthrough idea. “Having variables that talk about only pluses instead of specific locations turned out to be way better than talking about them in specific cells,” Heule told Quanta. In the end, ruling out 14 as a solution took less computer time than ruling out 13 had – and the pair had their answer.
“We had proved that 14 colors weren’t enough!” recalled Subercaseaux. “Really exciting! χρ(Z2) = 15!”
It had been three years since the young researcher had first seen the problem – and more than twenty since it had first been posed. But the question, more properly known as finding the packing chromatic number of the infinite square grid, finally had an answer – and that’s not all the pair had accomplished with their proof.
“For a point of reference on much we optimized, in 2010, Ekstein et al. proved a lower bound of 12, and it took them 120 days of computation,” Subercaseaux wrote. “Our techniques allow us to get the same lower bound in less than 10 seconds.”
That increase represents “a x1000000 factor improvement,” he noted. “Admittedly, hardware has improved substantially since 2010, but we went far beyond the hardware speed-up.”
Of course, as any math teacher will tell you, there was still one more thing to do: the duo had to check their workings. That took four months of careful verification and bug-fixing – almost as long as finding the solution itself – with the final result being posted on the arXiv preprint server in January 2023.
“This little problem, taken from a Facebook group, has given me so much joy!” Subercaseaux concluded. “Some frustration at times, but mostly joy […] This problem was definitely very addictive.”
The result can be found on the arXiv preprint server.
Source Link: Decades-Old, Infinitely Large Math Problem Gets Surprisingly Neat Solution