Sometimes, dramatic breakthroughs in niche areas of mathematics are like buses: you wait the best part of a century for one, and then three turn up altogether. At least, that’s the case for Ramsey Theory – a branch of combinatorics devoted to finding pockets of order within overwhelming randomness.
Following hot on the heels of major results in March and June of this year, a third problem regarding the so-called Ramsey numbers has now finally been vanquished.
The question: what is R(4,t)?
Now, technically speaking, what we’re looking for here is the minimum number of vertices v = R(4,t) such that all undirected simple graphs of order v contain a clique of order 4 or an independent set of order t. If that all doesn’t mean much to you, however, don’t worry: the easiest way to think about Ramsey numbers is via party planning.
No, seriously. Even to professional mathematicians, Ramsey numbers R(m, n) are known as the solutions to the Party Problem – that is, the minimum number of guests needed at a party to ensure that either m people know each other, or n people don’t. Take R(3, 3), for instance: that tells you the smallest party you can possibly throw in which either three people know each other or three people are strangers (the answer, if you’re hoping to host a mathematically interesting shindig in the near future, is six.)
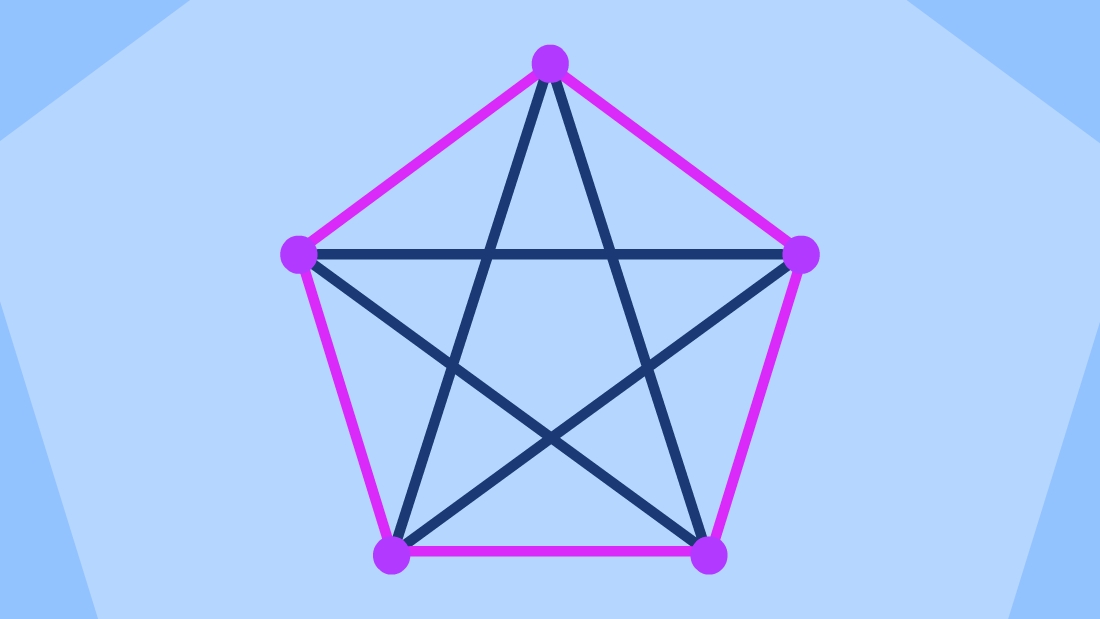
One way to visualize R(3, 3): suppose each vertex is a guest, a purple edge denotes two guests being friends, and a blue edge connects two strangers. With five guests, it’s possible that no group of three are either friends or strangers – otherwise, we would see a triangle with edges all of the same color.
Image Credit: IFLScience
Seems pretty simple, right? So you might think that finding R(4,t), the minimum number of guests to ensure that four of them know each other and some arbitrary number t are strangers, is equally straightforward. Instead, it’s stumped mathematicians for decades.
“Many people have thought about R(4,t) – it’s been an open problem for over 90 years,” said Jacques Verstraete, a researcher in combinatorics at the University of California San Diego and co-author of the new result, in a statement.
“But it wasn’t something that was at the forefront of my research,” he added. “Everybody knows it’s hard and everyone’s tried to figure it out, so unless you have a new idea, you’re not likely to get anywhere.”
Luckily, a new idea was exactly what Verstraete found in colleague and co-author Sam Mattheus – not a fellow combinatorist, but a geometer. Building on ideas already used by Verstraete to study R(3,t), the pair set about trying to solve R(4,t) using structures known as pseudorandom graphs – graphs that sort of look random, but in fact, are not.
“It turned out that the pseudorandom graph we needed [for R(4,t)] could be found in finite geometry,” explained Verstraete. “Sam was the perfect person to come along and help build what we needed.”
The answer: R(4,t) is roughly equal to t3 – that is, if you want to throw a party in which either four people know each other or t people are strangers, you need to invite around t3 people.
Now, you’ll notice we’ve given ourselves some wiggle room there, and that’s unavoidable: Ramsey Theory, and indeed combinatorics as a whole, has a tendency to produce calculations that are so mind-bogglingly massive and complex that we have to settle for estimates rather than exact solutions. We know that R(4, 15), to take an example at (pseudo) random, is somewhere between 153 and 417, but figuring out the precise answer would take eons of painstaking trial and error, and who really has the time for that?
In fact, even with pseudorandom graphs at their disposal, the problem “really did take us years to solve,” Verstraete said. “And there were many times where we were stuck and wondered if we’d be able to solve it at all.”
This is why, in Verstraete’s eyes, this breakthrough is really a message about the importance of perseverance. “One should never give up, no matter how long it takes,” he said. “If you find that the problem is hard and you’re stuck, that means it’s a good problem.”
The findings are currently under review with the Annals of Mathematics. A preprint can be viewed on the arXiv.
Source Link: Fiendishly Difficult Party-Planning Problem Finally Cracked Nearly A Century After It Was Posed