Imagine closing your eyes and rolling a billiards ball across a table. Where it goes; what angles it hits the sides at; how much it spins or swerves – all that is, for our purposes, basically random. And then, imagine you’re asked to roll it back to exactly its starting point. Could you do it?
Well, if you’ve read a recent paper from mathematicians Jean-Pierre Eckmann and Tsvi Tlusty, then yes, you could. In fact, it’s possible even if that ball was rolling around through three-dimensional space. “We show[ed] that almost every walk in SO(3) or SU(2), even a very complicated one, will preferentially return to the origin,” the pair announce in the paper.
It’s the kind of problem you might not have realized was still open in physics: to what extent is it possible to “undo” the movement of some body through space and get it back to where it started? And this isn’t just some niche headscratcher, either – there are numerous practical applications for such a “reset” function. “Rotations underpin nearly all modern technology and science,” points out a press release on the topic from Ulsan National Institute of Science and Technology (UNIST), where Tlusty is a distinguished professor in physics.
“From stabilizing satellites to decoding brain scans, from nuclear magnetic resonance to quantum computing, we constantly task rotators with performing intricate dances,” it explains. “This new result guarantees that, regardless of how complicated the choreography, there is always a way to return the system to its original pose.”
So, we know what you’re thinking: what actually is the answer? And as it turns out, it’s surprisingly easy: you “simply […] travers[e] the walk twice in a row and uniformly scal[e] all rotation angles,” the paper explains.
Let’s start with a basic example. Suppose you manage to hit the billiard in such a way that it spins round the table from six o’clock to nine o’clock. Now, you can pretty easily imagine a way to get it back to where it started: do the same thing again, twice, but each time one-sixth as far.
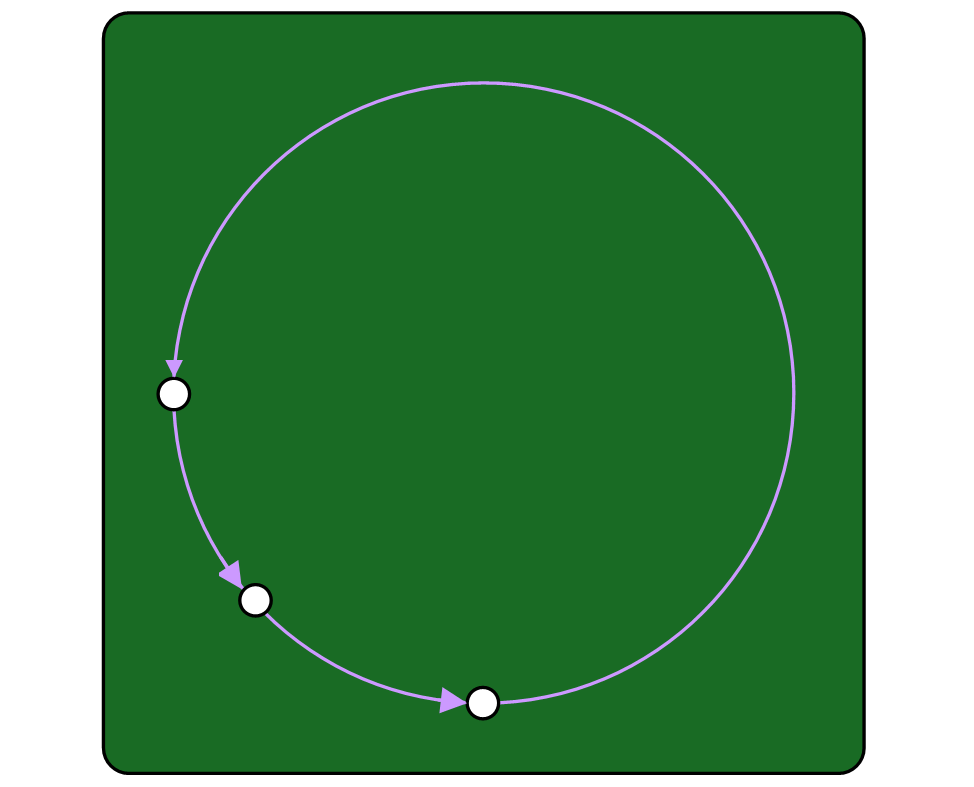
Think of the ball as being rotated about the center, first by 3pi/2, then by pi/4, then by pi/4.
Image credit: © IFLScience
You see the general idea? Now, imagine instead of that really simple path, you have a particle moving like this:
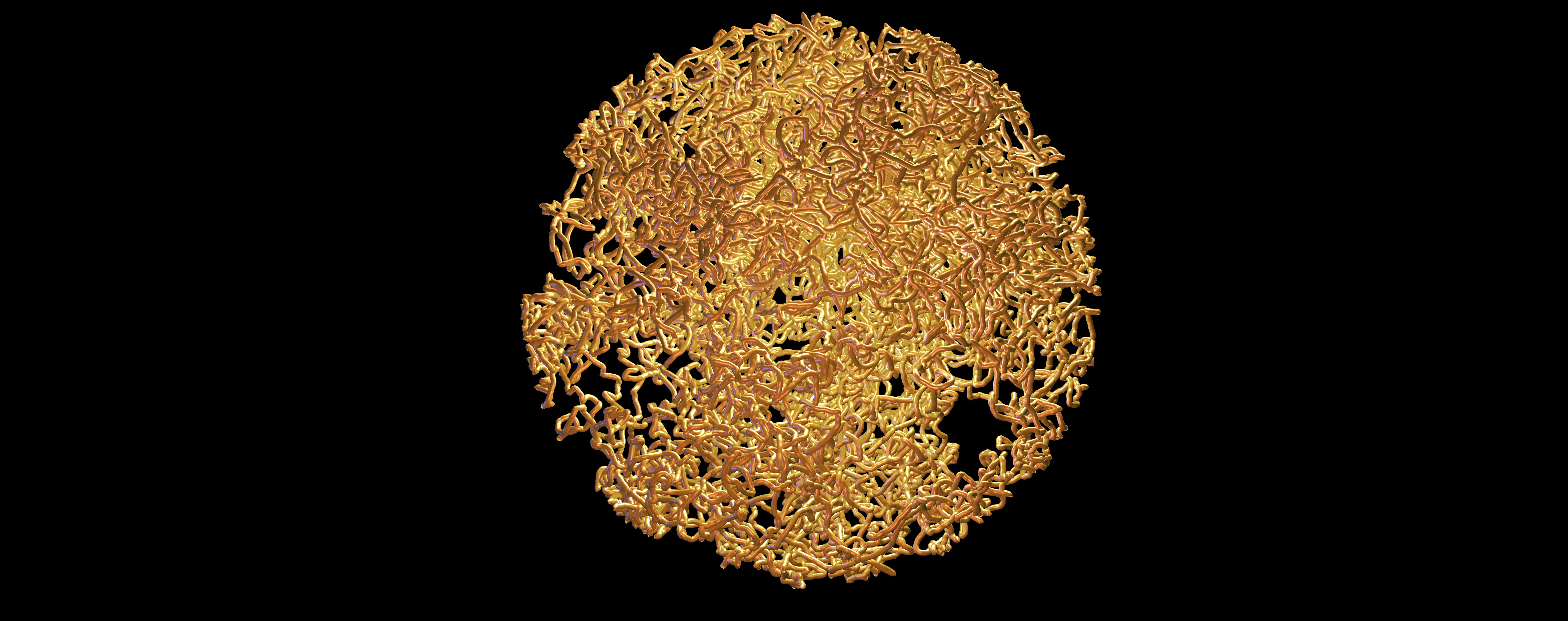
Reverse this.
Image credit: UNIST
Now that doesn’t look easy to undo – but that’s why the new paper is so important. “The astonishing answer is that it is always possible,” the press release says. “No matter how tangled the history of rotations, there exists a simple recipe: rescale the driving force and apply it twice.”
There are a couple of keys to how and why this works. First is the realization that these random walks being considered can all be expressed in terms of rotations – or, in math-speak, as operations within SO(3) or SU(2), two groups that you can think of intuitively as “moving around on and through a unit sphere”.
That’s important, because these groups have particular structures that make working with them easier – and, as the pair told New Scientist, they noticed that half-undoing a rotation performed within the sphere is equivalent to finding a path to some point on the sphere’s surface. That’s a lot easier than trying to get back to your starting point – if only because there are so many more points on the surface than your one single origin – and so, by combining a couple of older results on how to link together rotations and find solutions to multivariable equations, they deduced that finding these routes was nearly always possible.
It’s an impressive result – but more than that, it must also be a vindication for Tlusty and Eckmann themselves. As they note in their paper, they’ve been convinced of the theorem for a couple of years now – but for too long, a proof evaded capture. Now, the chapter is complete.
“A single application is never sufficient, but applying this doubled, rescaled force guarantees an exact return,” boasts UNIST. “Under this operation, the spin – or the qubit, or any rotor – will unfailingly come home.”
The paper is published in Physical Review Letters.
Source Link: Newly Discovered “Reset Button” Lets Mathematicians Undo Any Rotation