If pure math can teach us anything, it’s this: occasionally, your special interest might just change the world.
ADVERTISEMENT
For Joshua Zahl and Hong Wang, that special interest was the Kakeya conjecture. “I read a book in undergrad called A Panorama of Harmonic Analysis,” says Zahl, an associate professor in the University of British Columbia’s department of mathematics. “And I read about this in that book, and really was taken with it, and wanted to learn more […] that’s how the interest really started.”
Fast forward to today, and Zahl and Wang are now co-authors of a yet-to-be-peer-reviewed proof heralded by Eyal Lubetzky, chair of the mathematics department at the Courant Institute where Wang is an associate professor of mathematics, as “one of the top mathematical achievements of the 21st century.”
And it all started with a brainteaser about a needle.
The beginnings of a conjecture
It’s a peculiar truth of mathematics that the easier a problem looks on paper, the harder it often turns out to be. Take Fermat’s Last Theorem, for example: short and sweet enough to scribble in a margin, but a proof took more than 350 years and the development of multiple new fields of math to find.
The Kakeya conjecture is similar, if not quite as extreme. It goes back to 1917, when Japanese mathematician Sōichi Kakeya posed the following puzzle: given an infinitely thin needle of unit length, what is the smallest amount of space you can sweep out when rotating it through every direction possible?
In one dimension, the problem is trivial: the needle can’t move from its initial place, so the problem is either already solved or unsolvable, depending on perspective. But in two, things are already much more complicated.
ADVERTISEMENT
An obvious way to fulfill the “rotating through every direction possible” criteria in two dimensions is to simply spin the needle in a circle – but the resulting area is relatively large. A better solution, proposed by Kakeya himself, is to move the needle around a circle while it rotates, creating a sucked-in triangle shape known as a deltoid.
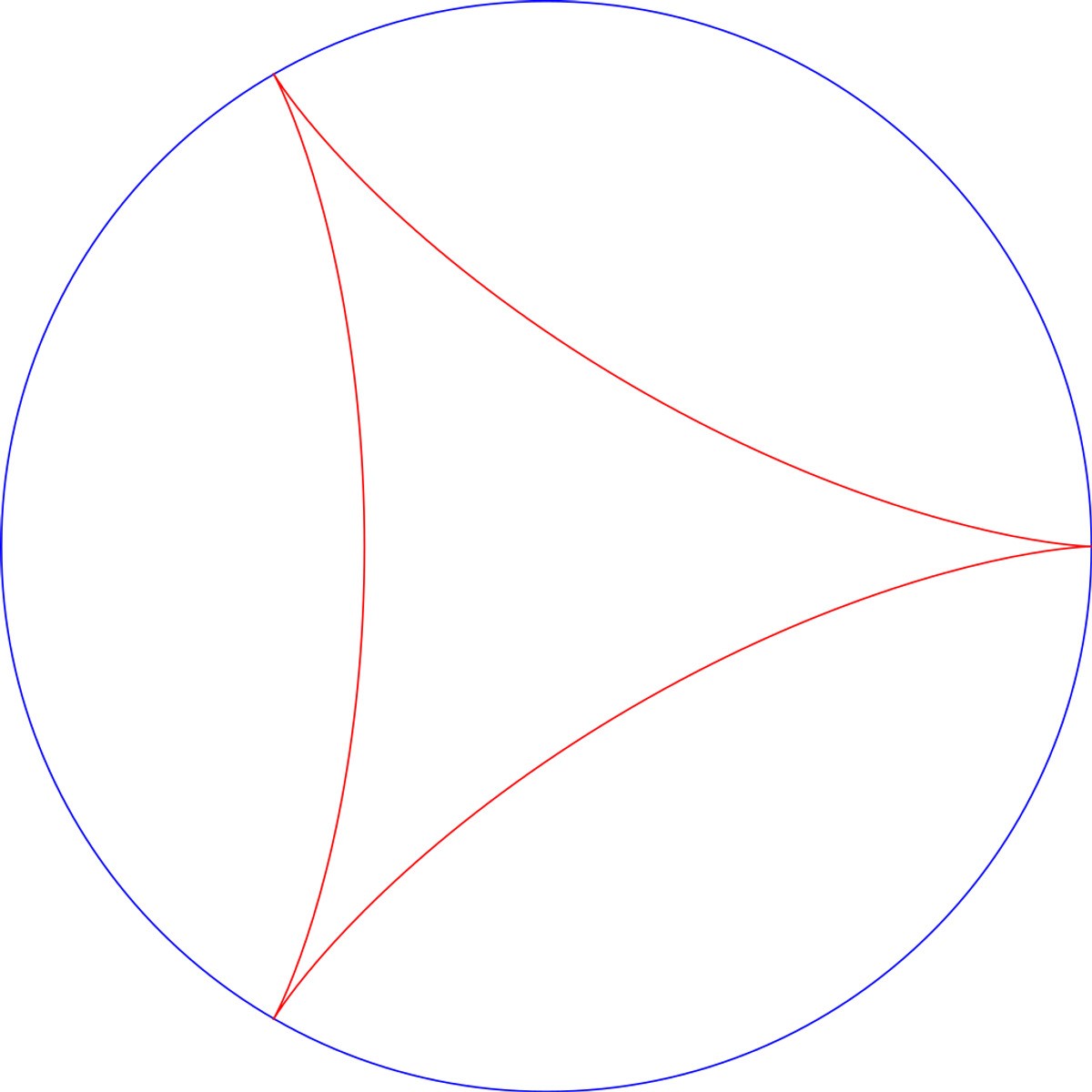
In blue: broke. In red: bespoke.
The area of this shape is much smaller – exactly half that of our circular first attempt, in fact. But it turns out we can do much, much better than that: in 1919, the Russian mathematician Abram Besicovitch showed that, with some mathematical ingenuity and a lot of needly finagling, it’s actually possible to sweep out a space with zero measure.
The resulting shapes – the so-called Kakeya sets – “have very counterintuitive properties. You could say pathological properties” Zahl says. “I mean, even the conjecture aside – the first time you read about a Kakeya set, if you’re naturally curious, you’re going to be pretty intrigued.”
“I suppose maybe the result itself is less important than, here’s an excuse for many people in the world to learn what a Kakeya set is,” he tells IFLScience.
A question of dimension
As unintuitive as Besicovitch’s result was, one thing is undeniable: you can’t get much smaller than zero. So, more than 100 years later, why are we still talking about the Kakeya conjecture?
Besicovitch may have shown that these shapes could take up zero space, but – to borrow a phrasing from Fields medalist and long-time Kakeya conjecture chaser Terence Tao – “not all sets of measure zero are created equal.”
Starting in the 1970s, with the work of Roy Davies, mathematicians started considering the problem from a new perspective. Rather than measuring the amount of space swept out by their infinitely thin needles, perhaps a different way of thinking about size was needed: what, they asked, would the dimension of these Kakeya sets be?
At first glance, that question may seem trivial. It’s a shape in three-dimensional space, ergo it has dimension three. Right?
ADVERTISEMENT
“It seem[s] very intuitive,” Larry Guth, Claude Shannon Professor of Mathematics at MIT and another veteran Kakeya conjecturist, told New Scientist last week. “It seem[s] like it must be true, but then it turns out to be very difficult to prove.”
It’s this, then, rather than Kakeya’s original statement, that mathematicians refer to when they talk about the Kakeya conjecture: the idea that these Kakeya sets should have the same dimension as the space they inhabit.
It’s a subtle reframing with an outsized impact. Rather than a niche intellectual curiosity, the newly stated problem now has deep connections to other areas of math: “there is, let’s say, a circle of questions that people are very interested in in harmonic analysis,” Zahl tells IFLScience – some “related to the behavior of the Fourier transform, and some related questions about the behavior of certain solutions to certain partial differential equations.”
Solve the Kakeya conjecture, and you break the first shell in a matryoshka of key questions in harmonic analysis. The problems “are all tightly connected,” Zahl explains. “The connection, as best I’m aware, was first discovered by Charles Fefferman in the – well, the paper was published in 1971, so late 60s, early 70s.”
Planes, grains, and all they reveal
With this new motivation, interest in the Kakeya conjecture flourished – but no definitive proof seemed forthcoming. In 1995, however, mathematician Thomas Wolff made something of a breakthrough: “he proved, amongst other things, that every Kakeya set in [dimension] three has Hausdorff dimension exactly five halves,” Zahl explains.
To a non-mathematician, such a statement can sound confusing, if not downright nonsensical – but fractional or irrational dimensions are actually nothing new in math. They’re a mainstay of fractal geometry, and with a shape as weird and unintuitive as a Kakeya set, it wouldn’t be totally surprising to find them cropping up again.
“Yeah, there were moments where we were very like […] it really might be two and a half,” Zahl tells IFLScience. “There were moments of doubt.”

This is what we’re dealing with, except like, asymptotic.
Still, they had good reason to believe in the conjecture. In 1999, Tao, along with collaborators Nets Katz and Izabella Łaba, had pushed the dimension measurement up a little bit – all the way from 2.5 to 2.500000001. It’s not much of a difference, objectively speaking, but that wasn’t really the point: the boundary had been crossed – and anyone tackling the problem going forward now had a roadmap to work from.
ADVERTISEMENT
“The way you do it is you say, okay, imagine the enemy gives you some particularly bad set – maybe a counter example to the conjecture, we could imagine – and we thicken it by this small amount of ‘delta’,” Zahl explains. Rather than being a collection of infinitesimally thin lines, now, we can think of the Kakeya set as being made of “uncooked spaghetti,” he says; “they have length one, but they’re quite thin, and they can overlap each other.”
Fittingly for a spaghetti-based analogy, a set like this is known to mathematicians as “grainy” – and it’s a necessary property for any counterexample to the Kakeya conjecture. Zoom in on the overlapping areas, and you find another such quality: “what was proved back in roughly 2005 is that, if this object was indeed a counter example to the conjecture, then the tubes passing through one particular point all have to be almost in a common plane,” Zahl tells IFLScience. “They all have to be roughly coplanar.”
There was just one more property to account for.
A sticky problem
That a counterexample to the Kakeya set should be “grainy” and “plany” was well-established – but Tao, Łaba, and Katz, who originally proposed these prerequisites, had a third item on the list: stickiness.
ADVERTISEMENT
To Kakeya scholars, that term has a particular meaning: a “sticky” set is one in which line segments that point in nearby directions must also be close to each other. It was, ironically, the slipperiest of the criteria, evading a proof for more than a decade – until, in 2022, Zahl and Wang unexpectedly showed the opposite. A sticky Kakeya set in three dimensions, they proved, must have Hausdorff and Minkowski dimension three – thus obeying the conjecture.
It was a hugely important breakthrough – but it wasn’t enough to prove the conjecture entirely. Next, the pair needed to examine the grainy, planey, but non-sticky cases, comparing their properties at various scales, and hopefully establishing a contradiction.
“A lot of this work comes from trying to understand the structural properties of what a counterexample to the theorem would look like,” Zahl tells IFLScience. “And if you can find enough of these structural properties and how they relate to each other, then maybe eventually […] you can show that [the counterexample] can’t exist.”
Three years and a couple hundred pages of various proofs later, the job was done.
Once in a century
With the uploading of Wang and Zahl’s paper to the arXiv preprint server, a wave of excitement rippled through the international mathematical community. Tao wrote about it on his blog; Katz lauded it as a “once-in-a-century kind of result.”
The paper “is a wonderful piece of mathematics,” said Guido De Philippis, a professor at the Courant Institute, in a statement. “[It] follows years of progress that has enhanced our understanding of a complicated geometry and brings it to a new level.”
“I am expecting that their ideas will lead to a series of exciting breakthroughs in the coming years,” he continued. “This result is not only a major breakthrough in geometric measure theory, but it also opens up a series of exciting developments in harmonic analysis, number theory, and applications in computer science and cryptography.”
Is such praise premature? After all, the result is technically yet to be peer-reviewed – but “to be clear, we don’t have serious concerns about the correctness of our proof,” Zahl says. That’s not hubris: after completing the thing, they sent it to just about everyone they could think of who might be able to find a mistake in it – and it came back clean.
ADVERTISEMENT
“We wanted as many of them as possible to sign off on it before we made it public,” he tells IFLScience. “With these things […] you need to have a lot of paranoia that you’ve made a mistake […] you don’t want to let yourself get excited until you’re sure you’ve done it.”
The paper can be read on the arXiv preprint server.
Source Link: "Once In A Century" Math Proof Threads The Needle On A Decades-Old Conjecture