Math, outside of a few pivotal scenes in the original Mean Girls, is not usually seen as a competitive sport. But… maybe it should be.
After all, from the earliest days of formal math, the discipline has been marked by – and often fueled by – challenges and rivalries. There are the Millennium Prizes, of course: solve one of those, and you can win $1 million – or refuse the prize and vanish into obscurity, like the only person so far to ever vanquish one. Those were based on David Hilbert’s list of 23 problems, posed to the mathematical community at large a century beforehand, and only a little earlier than that, we have Cantor and Kronecker (oh let’s be real, it was everyone and Kronecker) spitting insults at each other until the foundations of math are accidentally overhauled entirely.
And the earlier we go, the more combative math becomes. The 17th century gives us Newton and Leibniz instigating an intracontinental centuries-long Calculus War (real thing; look it up). In the Renaissance, public math battles were basically mandatory and could make or break a career – and because of that, we got the solutions to cubic equations and eventually the discovery of complex numbers.
It’s been fruitful, but why was it all so ruthless? Well, turns out, it’s kind of always been that way.
The first math lesson
You may have thought your math teachers were tough in school – but they have nothing on the first guy on record. Socrates, an Athenian philosopher born in the fifth century BCE, was so prolific a scholar and teacher that we still talk about his Socratic method of instruction today – but he was also the original “debate me” bro, so annoying to everybody around him that literally his whole city ganged up together and told him to either shut up already, or die (famously, he chose the latter).
Take his challenge to Meno, for example. A simple question about the nature of knowledge becomes a bet between two gentlemen over whether or not an uneducated kid can be taught lofty ideas, and no, this isn’t just an ancient Greek My Fair Lady – that’s Pygmalion you’re thinking of.
The story starts with Meno asking Socrates about knowledge, presenting him with what seems to be a paradox. “How will you enquire, Socrates, into that which you do not know?” he challenges. “What will you put forth as the subject of enquiry? And if you find what you want, how will you ever know that this is the thing which you did not know?”
It’s a good question, but Socrates has an answer immediately ready: your soul, he argues, is immortal and many-times reincarnated, and it’s already learned everything possible at some point or another. Learning, therefore, isn’t a question of discovering new information, but of remembering everything you forgot when you were a stupid baby.
Meno, understandably, responds to this with the ancient Greek equivalent of “sounds fake tbh”, and so Socrates throws down a challenge. “Call one of your numerous attendants,” he tells Meno, “that I may demonstrate on him.”
All Greek to me
A slave boy is summoned, and Socrates sets about teaching him some basic geometry. “Tell me, boy, do you know that a figure like this is a square?” he asks, and “[do] you know that a square figure has these four lines equal?” The boy says yes, so he ups the difficulty: “If one side of the figure be of two feet, and the other side be of two feet, how much will the whole be?” he asks.
Once the answer is found, we move into the second act of She’s All That: the humiliation. This square has an area of four – so, Socrates asks the kid, how big is the area of a square twice this size? And, when the correct figure of eight is given, the coup de grâce: “try and tell me the length of the line which forms the side of that double square,” he says.
The boy – who, remember, is a slave kid with zero education – suggests that the answer must also be twice as much as the original. That’s wrong, so after a brief aside in which he loudly tells Meno what an idiot this child is, Socrates tells him why. Let’s double that line, he says, and we’ll see how big the resulting square actually is. “Is it not four times four?” he asks the boy, “And four times is not double […] But how much?”
Eventually, the boy figures out that doubling the length of the sides of a square results in quadrupling the area – but that still leaves the original question unanswered. How much bigger should the side length be to double the area?
A surprise theorem!
So, this is where the story gets… kind of cool, at least from a math nerd perspective. Socrates draws a diagonal across the original square, cutting it in half. Then, he draws three identical copies, arranged so that together they make a square four times the original area.
“How many times larger is this space than this other?” he challenges the boy. “Four,” comes the reply.
“And does not this line, reaching from corner to corner, bisect each of these spaces?” Socrates points out about the drawn diagonals. “And are there not here four equal lines which contain this space? […] Look and see how much this space is.”
What’s the answer? As Socrates and the kid work out, it’s half of a two-by-two square, four times – making eight overall. This is the side length you need to double the area – but in finding that answer, we’ve also discovered something that, for the time, was the statest of state-of-the-art math.
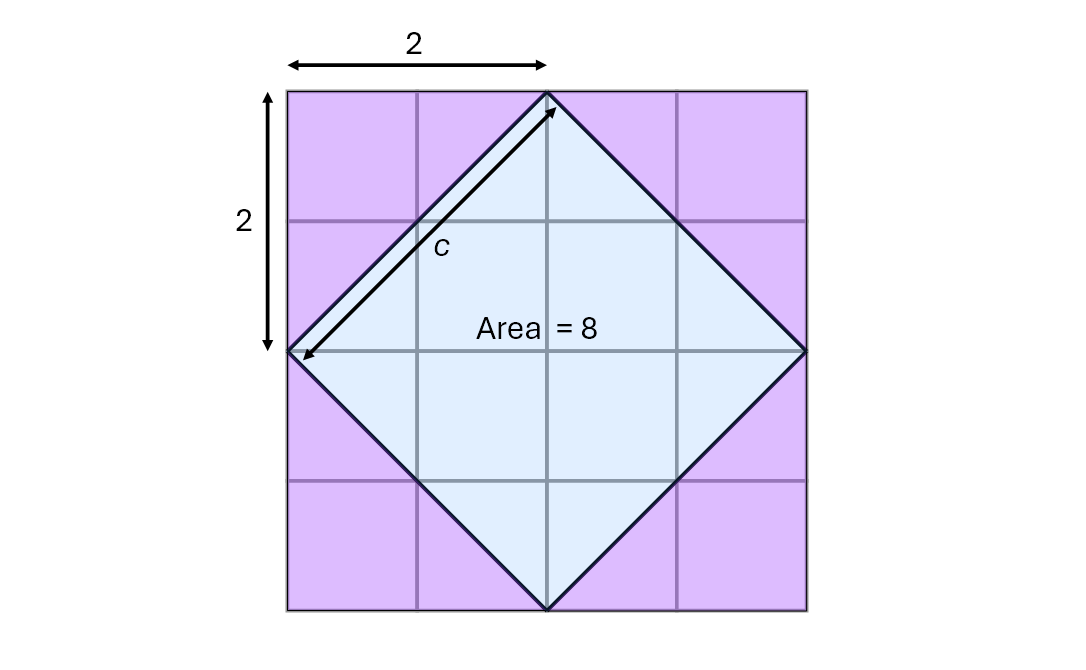
What is the length of c?
Image credit: IFLScience
Recognize it? It’s a geometric representation of Pythagoras’s Theorem! And it’s probably one of the earliest ones, too: it’s the same method that some scholars think may have been used for the first formal proofs of the rule. Once again, an impromptu math fight – albeit an incredibly one-sided one – has produced a new and incredibly important result, setting off a pattern that would be replicated again and again throughout the ages, even up until the modern day.
Which is, overall, not bad for a slave boy with no education. Don’t you think?
Source Link: The First Math Challenge (Or: Why The History Of Math Is Full Of Infights And Feuds)