When a comet starts to approach the Sun or a planet is newly discovered orbiting another star, one of astronomers’ most important questions is how eccentric the orbit is. Since most non-scientists don’t know what this means, there’s always a question of whether to explain what is meant in articles about the discovery, or to avoid the word. Perhaps it’s time for a more detailed explanation.
A brief history of orbits
ADVERTISEMENT
In classical times and through the Middle Ages, it was believed that planets orbited the Earth on perfect spheres. When more detailed observations of their orbits raised problems with this, adjustments were made, with smaller spheres thought to modify the great ones. As tracking of planets’ movements improved, so many smaller spheres were required that models started to resemble an old Heath Robinson cartoon, or something from Wallace and Gromit.
Those who studied the problem, whether they still thought the planets orbited the Earth or favored a Sun-centric model, recognized that something was wrong, but couldn’t find an alternative that worked.
That was until Johannes Kepler proposed his three laws, which described planets orbiting the Sun not in circles, but ellipses. Ellipses look a little like a circle made of a flexible material that someone has grabbed on opposite sides and stretched out so that it is much longer in one direction than the other. Planets move more slowly in the more distant parts of their orbit.
The invention of the astronomical telescope five years later confirmed Kepler’s work. It also provided examples we could witness from the outside like the orbits of Jupiter’s largest moons around their planet, confirming elliptical orbits are universal, not just a property of things that directly orbit the Sun.
Eighty-three years later, Isaac Newton provided a physical explanation for why objects would forgo circles, a two-dimensional representation of what was considered the perfect shape, in favor of ellipses.
What is an ellipse?
Ellipses are defined as curves that surround two focal points. At any point on the ellipse, the sum of the distance to both is a constant. If the two focal points are together, you get a circle, and the further they are apart, the longer and thinner the ellipse will be.
ADVERTISEMENT
Kepler thought the Sun was located at one of the focal points of the ellipse, and for small planets, that’s pretty much true. However, you may have read that technically Jupiter does not orbit the Sun. That means that rather than the Sun being at the focal point, the center of mass (barycenter) of the Sun-Jupiter system is at the focal point instead. That’s true for any orbiting object, but Jupiter’s mass is large enough that the system’s barycenter is outside the Sun, instead of within it.
The eccentric part
Even among the original planets, there are wide variations in the ellipses they follow. Venus has an orbit so close to circular that Kepler could probably have made himself believe any deviations were errors in measurement if it were the only planet he was investigating. The difference between its closest approach to the Sun is not much more than 1 percent closer than its furthest point.
Mars, on the other hand, has a much more stretched-out orbit. At its most distant, it is 16 percent further from the Sun than at its closest. That’s why some oppositions of Mars, when the Earth passes between Mars and the Sun, are much brighter and more impressive than others. The distance between the two planets is much smaller when we pass Mars near its closest approach (perihelion). It’s fortunate that Kepler was told to make finding the orbit of Mars his primary focus.
An orbit’s deviation from circularity is known as its eccentricity (e) and measured with a value between zero and 1. A perfectly circular orbit has e=0.
ADVERTISEMENT
Venus’s eccentricity is 0.007. Earth’s is also low at 0.017, which is why our seasons are mostly about axial tilt, rather than distance from the Sun. Meanwhile, Mars has an e of 0.0934.
The value is calculated as the square root of 1 minus the square of the distance between planet and star at its closest divided by the square of that distance at its greatest.
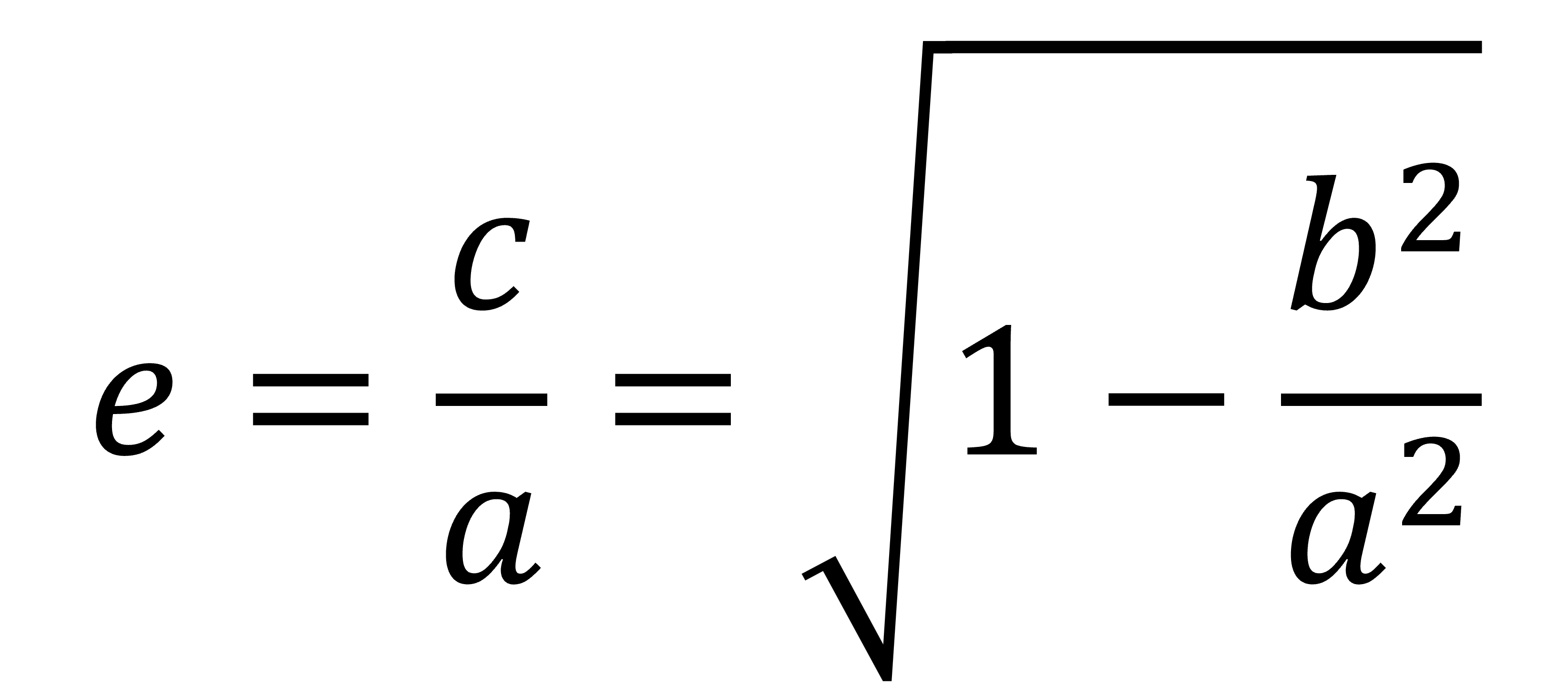
In the formula for e, b is the shortest distance from orbiter to the orbited, and a the greatest.
Image credit: IFLScience
There’s no specific number above which an orbit is considered eccentric; instead, all orbits are eccentric to a degree. A bit like people, really.
Really eccentric orbits
Mercury has the most eccentric orbit of any planet (since Pluto’s demotion) at 0.206, but it’s close to circular compared to that of most comets, quite a few asteroids, and some other stars’ planets.
ADVERTISEMENT
Long-period comets that visit the inner Solar System just once every hundred thousand or million years often have eccentricities above 0.99.
If an object is not orbiting the Sun at all, but merely passing through, it has a hyperbolic trajectory, and its e value is greater than 1. When ‘Oumuamua was first observed, astronomers raced to collect data to allow them to calculate its eccentricity. Most initial estimates produced values greater than 1, indicating interstellar origins, but these came with margins of error. Taking the lowest end of these ranges, some astronomers concluded the true value was probably below 1, which would have made it just another comet from our own Oort cloud. Fortunately, they were wrong and ‘Oumuamua was a true visitor from the stars.
Hearing the words “eccentric orbit,” it’s tempting to imagine an object drunkenly swerving through space, so we’re sorry to reveal a duller truth. Some objects’ orbits do veer around a bit, for example, when they pass near a planet’s gravity well, or when the release of some gas gives a comet a push. Important as those events can be, they’re not what we mean when we say an orbit is highly eccentric.
Source Link: What Is An Eccentric Orbit, And Which Astronomical Objects Have One?