Imagine the situation: you walk into an interview, and they hit you with an unexpected question. Which number is bigger, they ask: 3.14π, or π3.14?
Now, other than being annoyed that this is being asked for an entry-level job at a gas station, what’s the answer? Don’t worry, we don’t expect you to work it out by hand – or at all, actually. Thanks to a useful mathematical rule, you can pick the right answer almost immediately – no pen, paper, or pocket calculator necessary.
So, what’s the rule? It’s that, generally, exponentials beat multiplication. This is the area of math known as asymptotics, which deals with the behavior of functions as the numbers they act on shoot off to zero and infinity – and there’s a whole hierarchy of how fast they grow that student mathematicians have to work into their muscle memory before they can graduate.
It goes like this: assuming x and n are positive (the other cases aren’t too difficult to adapt), we have the slowest growth being… well, technically the slowest growth comes from a constant function, because it doesn’t grow at all. After that, however, we have logarithmic functions as the slowest growing: they do tend to infinity, but they get there really, really slowly.
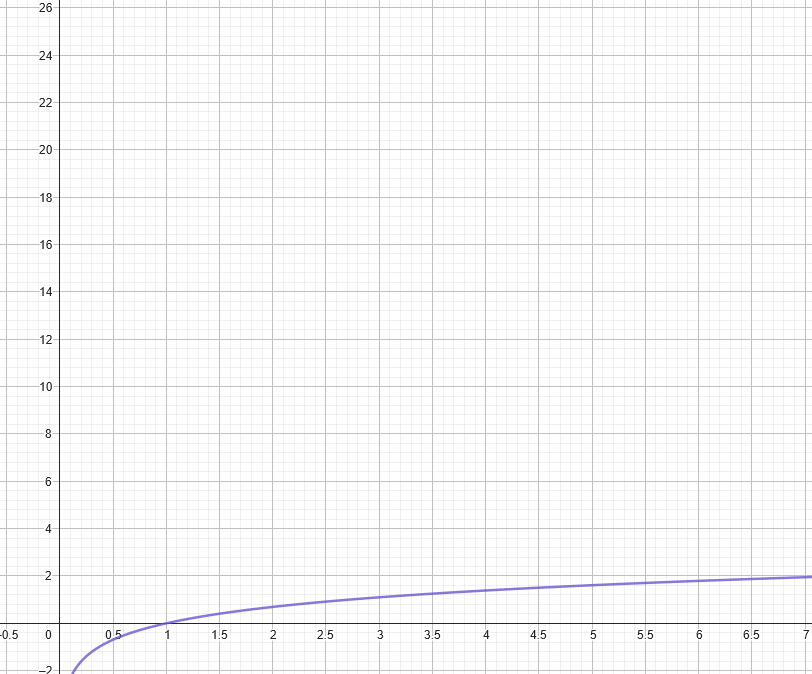
Yawn.
Image credit: IFLScience, using GeoGebra
Then there’s linear functions: nx. Basically, these are functions where you’re just doubling the input, tripling it, or suchlike. It’s technically a polynomial, so it’s often absorbed into the next category: polynomial functions xn – things like x2, x3, x3.14, xπ (put a pin in those last two).
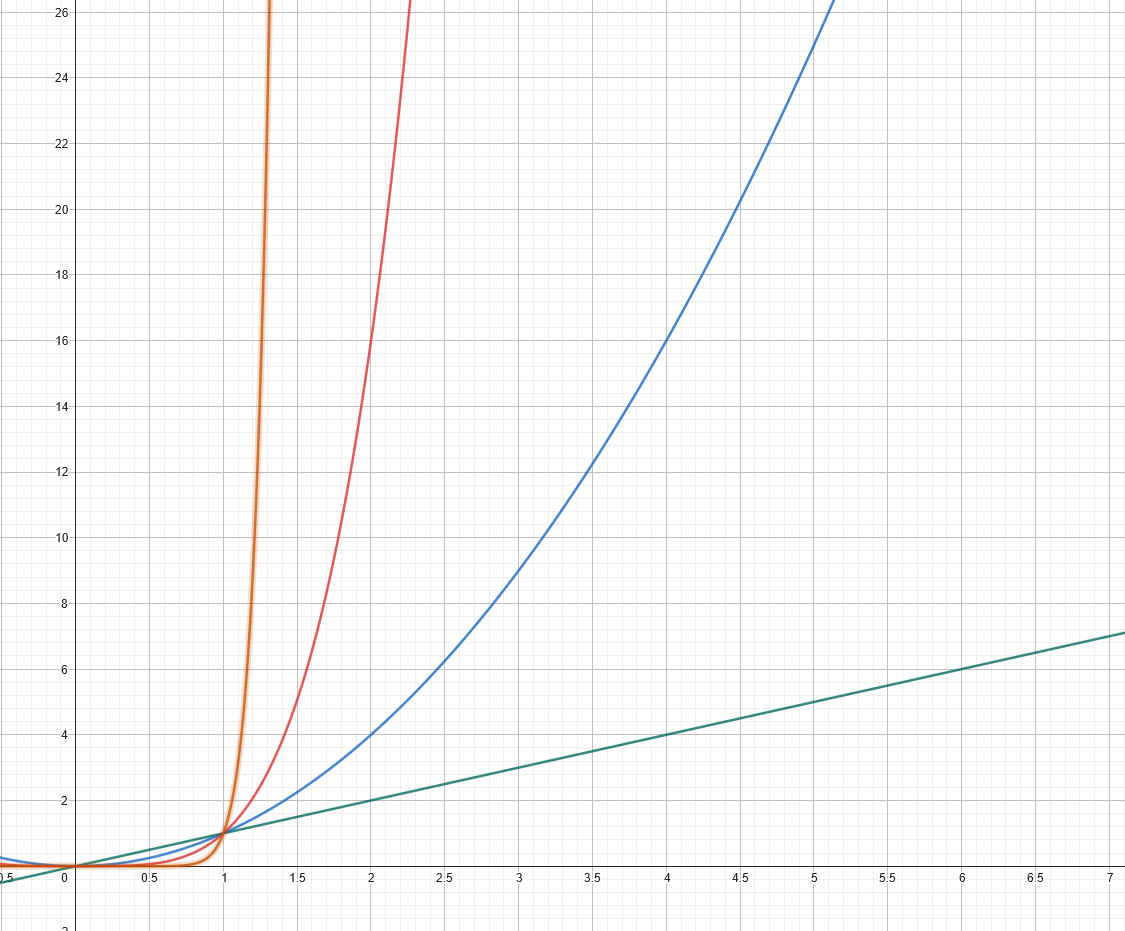
Green: y=x; blue: y=x^2; red: y=x^4; orange: y=x^12.
Image credit: IFLScience, using GeoGebra
Next come exponential functions – here we swap around the polynomials to get nx.
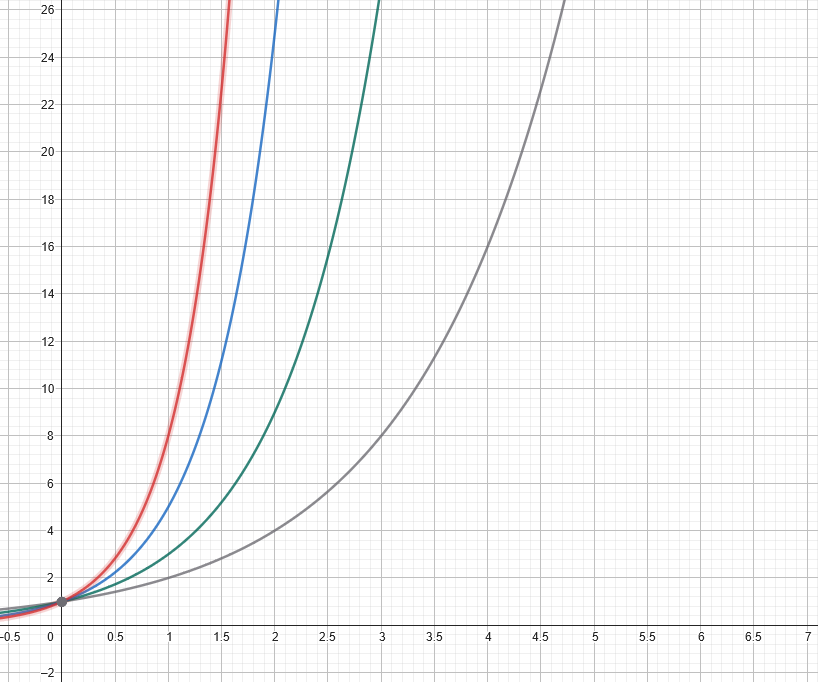
Grey: y=2^x; green: y= 3^x; blue: y= 5^x; red: y= 8^x
Image credit: IFLScience, using GeoGebra
And finally, we have factorials: x!, or x multiplied by every number below it (shut up, math nerds, we’re ignoring the gamma function today).
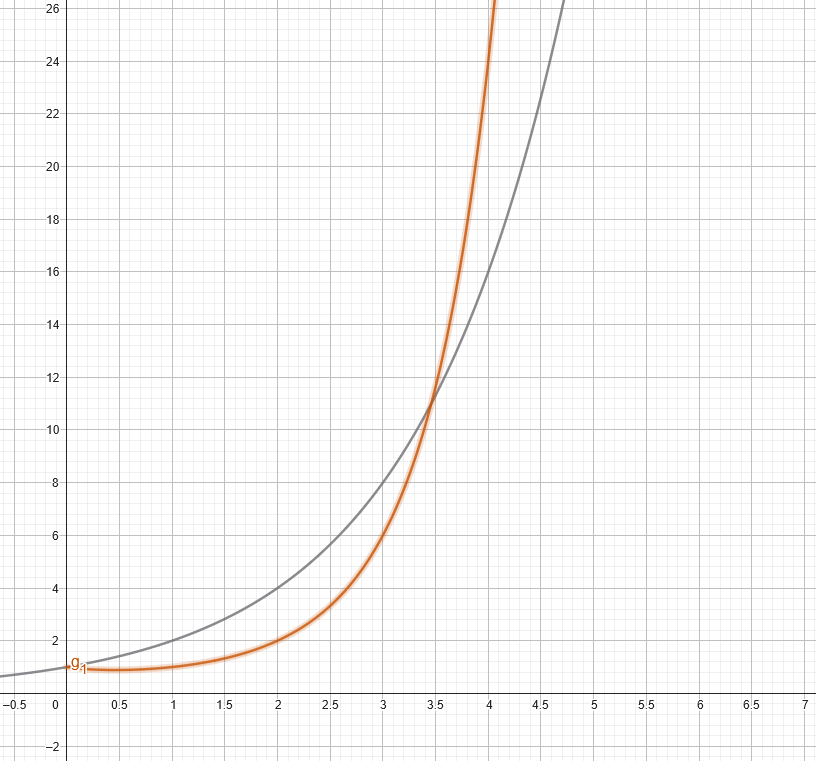
Orange is y=x! – grey is y=2^x, for comparison.
Image credit: IFLScience, using GeoGebra
Now, that’s not an exhaustive list – factorials can actually be beaten by, say, xx, for example – but it’s the basic setup. And we can use this to figure out the answer to the original question: we can see that generally, nx grows faster than nx – or to put it another way, whatever is in the exponent has more of an effect than whatever is in the base.
And since pi is greater than 3.14 – even if it’s only by less than two thousandths – that means the expression with π as the exponent is going to win.
Now, a caveat before you start busting this rule out willy-nilly: it doesn’t work below e. Try the same trick with 2 and 2.5, for example, and it reverses: we have 22.5 = 5.66, but 2.52 = 6.25.
Nevertheless, for this job interview, the general rule holds out. And if you’re wondering what the answers really are, we can finally prove our case: 3.14π = 36.404, while π3.14 = 36.396. They’re close, but the greater exponent has clearly won out. What’s our starting salary, boss?
Source Link: Which Number Is Bigger, 3.14^π Or π^3.14? Here's How To Solve It