It’s a theorem proven time and time again: there ain’t no party like a mathematicians’ party. The latest demonstration of the lemma that math is the subject for those who like to party hearty is an interactive map – definitely not produced as a last-second excuse for charging a pub crawl to the university account, we promise – laying out the ideal route for visiting every single one of South Korea’s 81,998 bars in one go.
“It would be a very long pub crawl,” says an arguably understated write-up from William Cook, a professor of combinatorics and optimization at the University of Waterloo in Canada, and one of the mathematicians who solved the problem. “The total walking time for the round trip is 15,386,177 seconds, or 178 days, 1 hour, 56 minutes, and 17 seconds.”
“You will need to stop for plenty of drinks along the way,” he adds.
Now, as fun and useful as this information is, the point is not actually to provide Korean drunkards with an optimized route for a six-month-long bender. It’s a demonstration of a real math puzzle with roots going back at least two centuries: the traveling salesman problem – aka, “what’s the quickest way of visiting every point on a map exactly once and returning to the original point?”
Let’s consider a simple example. Here’s a (very simplified) map of a few North American cities:
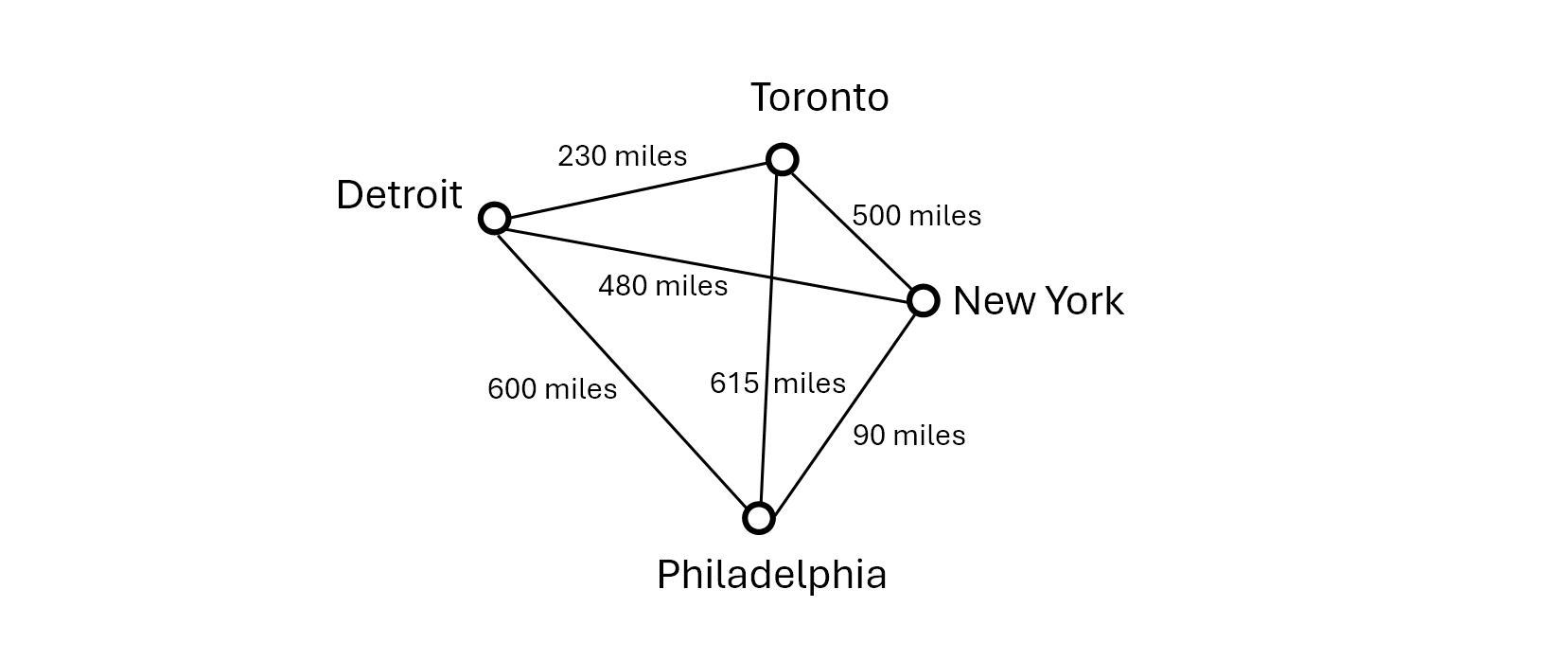
It’s not accurate DO NOT COME FOR US.
Image credit: ©IFLScience
So, here’s the question: let’s say you live in New York. What’s the fastest way for you to visit all three neighboring cities and get back home again?
Now, you might be tempted to go for the obvious:
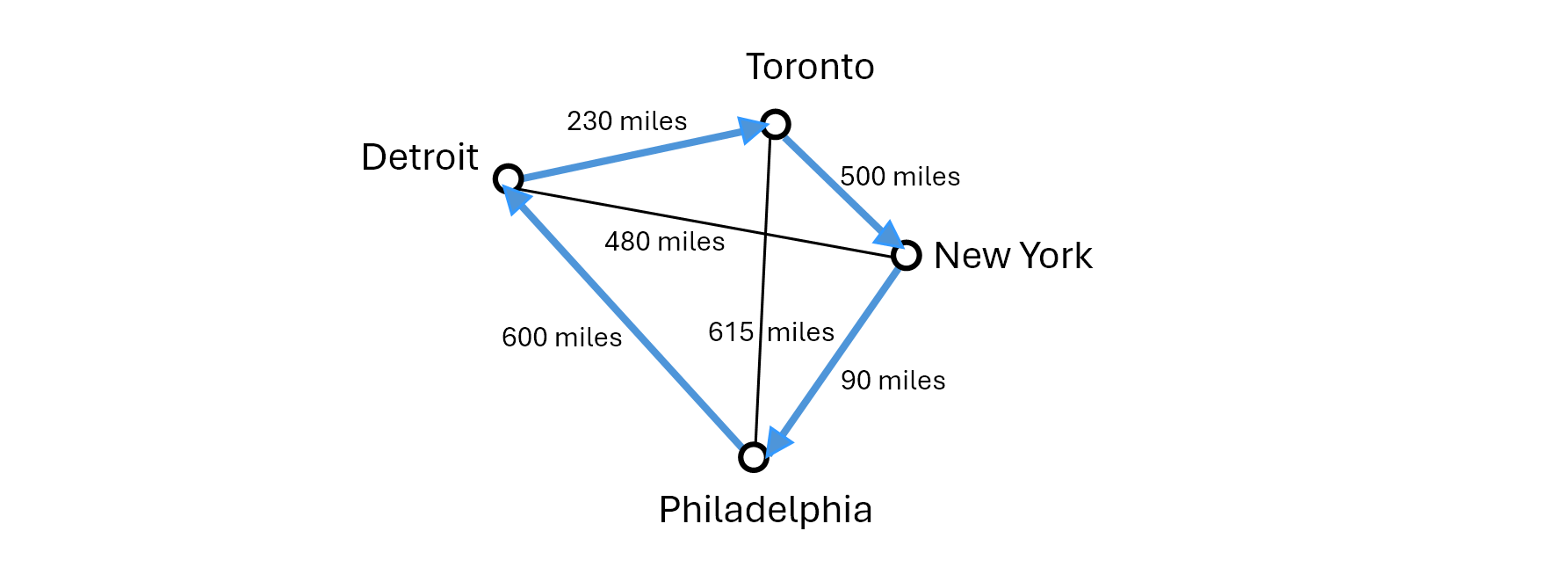
2,285 kilometers, or 1,420 miles total.
Image credit: ©IFLScience
But in fact, there’s a slightly faster route:
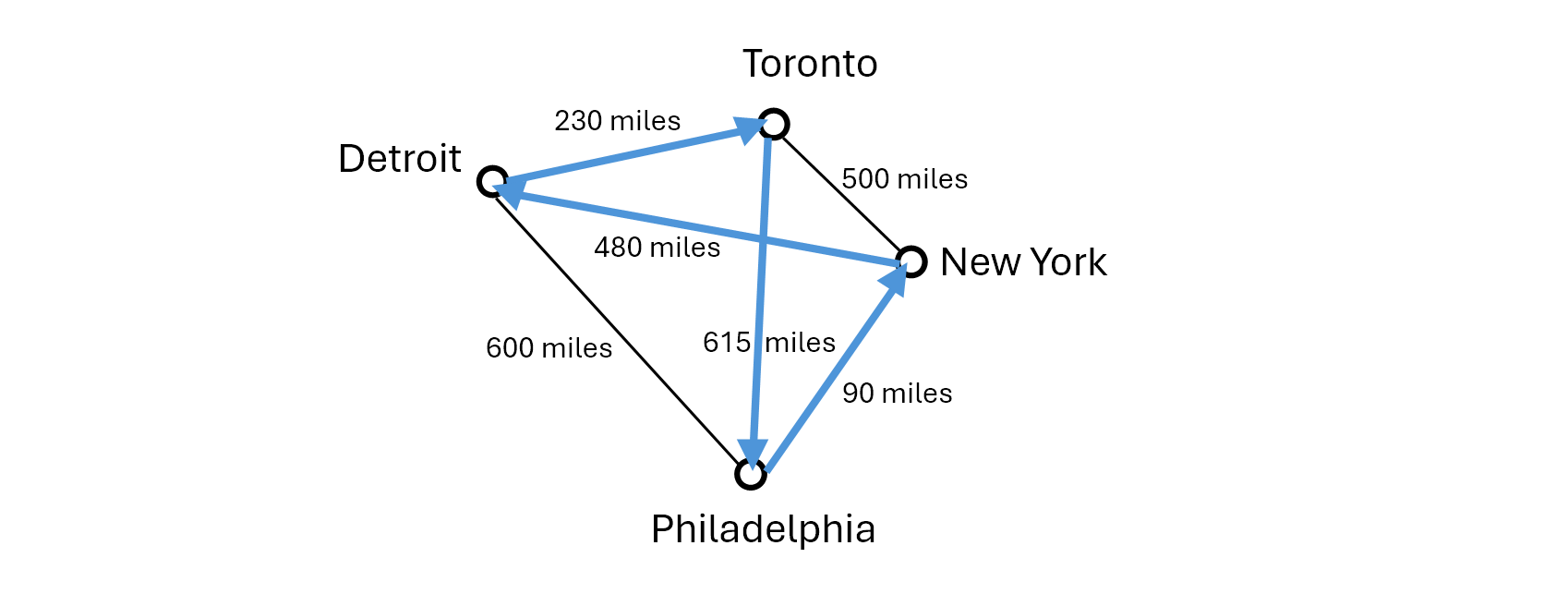
2,277 kilometers, or 1,415 miles.
Image credit: ©IFLScience
So, big deal, you might think – that was pretty simple. But like so many math questions, the traveling salesman problem is way, way easier stated than solved. It’s what’s known as “NP-hard”, meaning the amount of effort needed to solve any version of it increases exponentially faster than the complexity of the problem itself.
Like calculating ever-longer estimations of pi, therefore, solving various traveling salesman problems has become more of a sly boast than a genuine mathematical endeavor – a way to show off that your algorithms and code can cope with a problem of that magnitude and spit out a solution faster than the heat death of the sun.
“We use large examples of the traveling salesman problem as a means for developing and testing general-purpose optimization methods,” admits Cook. “The world has limited resources and the aim of the applied mathematics fields of mathematical optimization and operations research is to create tools to help us to use these resources as efficiently as possible.”
With 81,998 bars in South Korea to visit, “the number of tours in [this] case is roughly 2 followed by 367,308 zeroes,” Cook explains. Even if you could check a million tours per second, that would still dwarf the amount of time from the Big Bang until now – and by, like, a lot. It’s truly difficult to properly explain how gigantic this number is.
But this is where the impressive bit comes in. “This huge number of possible solutions is frightening, but it doesn’t mean we can’t solve [it],” Cook wrote. Simply put (or at least, as simply put as these things can be) their approach relied on two main techniques: first, the Lin-Kernighan heuristic – pretty much the best algorithm out there for finding traveling salesman solutions – and second, a tool called the “cutting-plane method”, in which you “send half a salesman along both branches of [a] fork” in the tour, Cook explained.
It is, no doubt, a very impressive feat – and, with the best route through more than 3,361,795,000 point-to-point travel times calculated, a powerful vindication of the researchers’ approach to the traveling salesman problem.
It’s just a shame that, after visiting nearly 82,000 bars in an incredibly efficient amount of time, nobody will be sober enough to understand it. Cheers!
Source Link: Mathematicians Figure Out How To Best Complete 80,000-Bar Pub Crawl