In science and mathematics, it has been a fairly common occurrence for two different people/teams to be working on the same problem, and invent the same solution. After all, both fields are concerned with finding underlying rules that govern math and science, it shouldn’t be surprising that these would occasionally be discovered independently.
ADVERTISEMENT
On very rare occasions, people can independently come up with something that has been discovered centuries prior.
“Isaac Newton just copied me,” one Redditor claimed this week, for instance. “I’m a high schooler and I’ve been working on this math ‘branch’ that helps you with graphing, especially areas under a graph, or loops and sums, cause I wanted to do some stuff with neural networks, because I was learning about them online. Now, the work wasn’t really all that quick, but it was something.”
This is an area which, while a high-schooler may not have heard of it, is a pretty significant tool within math.
“Just a few weeks ago we started learning calculus in class,” Redditor ThatGuyWhoLikesMoney added. “Newton copied me. I hate him.”
While there’s no shame in a high-schooler rediscovering math rules – in fact, as many commenters agreed, that’s pretty awesome – others pointed out that academics have made the same mistake, and in peer-reviewed journals.
In 1994, a paper published in the journal Diabetes Care appeared to claim the discovery of “Tai’s Model”, a “mathematical model for the determination of total areas under curves from various metabolic studies”. The paper was aimed at correcting the “deficiency of under- or overestimation of the total area under a metabolic curve”.
ADVERTISEMENT
In order to do so, the author outlined a method of calculating the area underneath a curve through the clever use of known shapes.
“The strategy of this mathematical model is to divide the total area under a curve into individual small segments such as squares, rectangles, and triangles, whose areas can be precisely determined according to existing geometric formulas,” the author, Mary M. Tai, explains. “The area of the individual segments are then added to obtain the total area under the curve.”
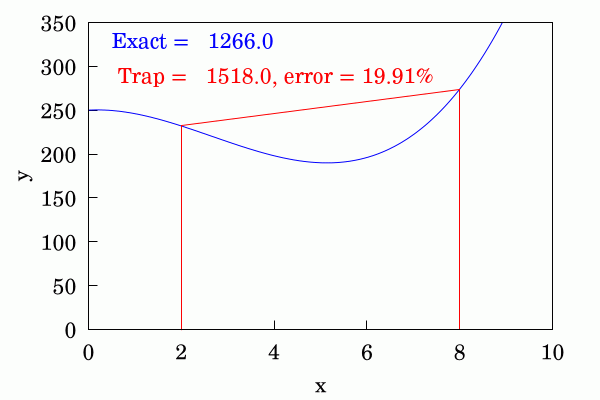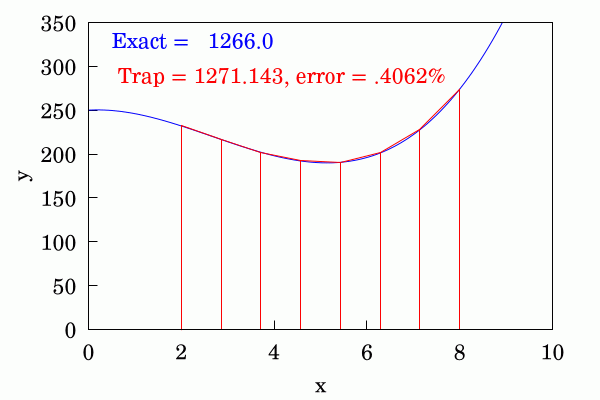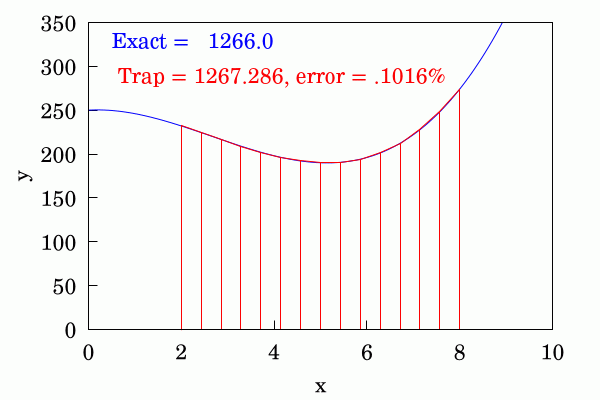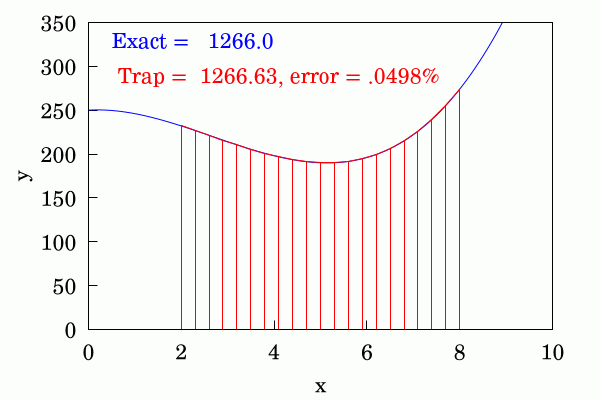
Graph showing how the area under a curve can be calculated using the trapezoid rule.
While a pretty smart way of doing it, and certainly a helpful way of calculating the area underneath a curve, there was just one small problem that mathematicians took offence with; the method had been known about for centuries. As such, several mathematicians replied in letter form, explaining that they were reluctant to rename it “Tai’s model” following the new paper.
“I commend Tai for producing a correct method for calculating the total area under the curve. It uses the trapezoid rule, a basic geometrical concept, which is that the area of a trapezoid is the mean of the length of the two parallel sides times the width,” one reply explains. “This method has been used by those of us in the field for many years and, in my opinion, does not need a new name.”
ADVERTISEMENT
“The trapezoidal rule is used in undergraduate calculus courses to illustrate and develop the calculus of definite integrals. Calculus students begin estimating area under a known curve by dividing the x-axis into small intervals and totaling the area of the resulting trapezoids,” another letter explains. “The exercise demonstrates that the error in the area calculation decreases as the length of the x-axis intervals is decreased. Definite integrals are then defined by taking the limit of the trapezoid’s summation as the x-axis intervals go to zero.”
Some were explicit in pointing out “that the trapezoidal rule was known to Isaac Newton in the 17th century”. Yet more replies complained about Tai’s mathematical notation (using a small x rather than a capital) but did not really question the validity of the rule, which is well-established.
Tai responded to the letters, explaining that she had derived it independently.
ADVERTISEMENT
“During a session with my statistical advisor, and after examining several alternative methods, I worked out the model in front of him. The concept behind it is obviously common sense, and one does not have to consult the trapezoid rule to figure it out,” Tai explained. “The trapezoid rule is really not Nobel Prize material, such as the double helix or jumping genes. I also used the formulas to calculate the areas of a square or a triangle without knowing whose rules were being followed.”
Tai went on to explain that she had not published the model as a “great discovery or accomplishment”, but because colleagues at the Obesity Research Center of St Luke’s-Roosevelt Hospital Center and Columbia University where she worked had begun using it for ease, and had started to call it “Tai’s formula”.
“Later, because the investigators were unable to cite an unpublished work, I submitted it for publication at their requests,” Tai added. “Therefore, my name was rubber-stamped on the model before its publication.”
The dispute seems to have gone down in relatively good humor, with the main article being cited 565 times, likely in jest by further researchers who needed to use the trapezoidal rule. As with the high-schooler above, there is no shame in rederiving mathematical rules which can be traced back to Babylonian times. But that’s why it’s best to check with the literature, before you get a lot of letters from mathematicians.
Source Link: In 1994, A Paper Claimed To Invent A Key Mathematical Rule Established Centuries Ago